점화식
- 어떤 함수를 자신보다 더 작은 변수에 대한 함수와의 관계로 표현한 것

- 자기호출을 사용하는 함수의 복잡도를 구하는데 유용하게 쓰인다.
병합 정렬의 수행 시간

수행시간의점화식
T(n) = 2T(n/2) + 오버헤드
크기가 n인 병합 정렬 시간은 크기가 n/2인 병합 정렬을 두 번하는 시간과 나머지 오버헤드(두 개 정렬 결과를 병합하는 시간)를 더한 시간이다.
점화식의 점근적 분석 방법
1. 반복 대치
- 더 작은 문제에 대한 함수로 반복해서 대치해 나가는 해법
2. 추정후 증명
- 결론을 추정하고 수학적 귀납법으로 이용하여 증명하는 방법
3. 마스터 정리
- 형식에 맞는 점화식의 복잡도를 바로 알 수 있다.
반복 대치
예시 1: 팩토리얼

- C부분이 오버헤드라고 할 수 있다.
예시 2

- 해당 크기 만큼(n) 오버헤드가 걸린다.
- n = 2^k로 표현한다. (k = logn)
추정 후 증명
- 식의 모양을 보고 점근적 복잡도를 추정한 다음 그것이 옳음을 귀납적으로 증명
추정이 맞는 경우

추정 함수를 잘못한 경우 T(n) ≤ cn

- 하지만,
T(n) ≤ cn -2로 설정하면 옳게 나온다. (O(n)이 맞다.)

마스터 정리
T(n) = aT(n/**b**) + f (n)와 같은 모양을 가진 점화식은 마스터 정리에 의해 바로 결과를 알 수 있다. (b가 수행시간에 큰 영향을 준다.)- 배수로 변하는 식만 사용가능하다. (팩토리얼은 사용할 수 없음)

- 정리: f(n)과 h(n) 중 더 큰 것을 수행시간으로 결정한다. 다만, 같은 경우엔
Θ(h(n)log n)로 수행시간을 정한다.
마스터 정리 예시
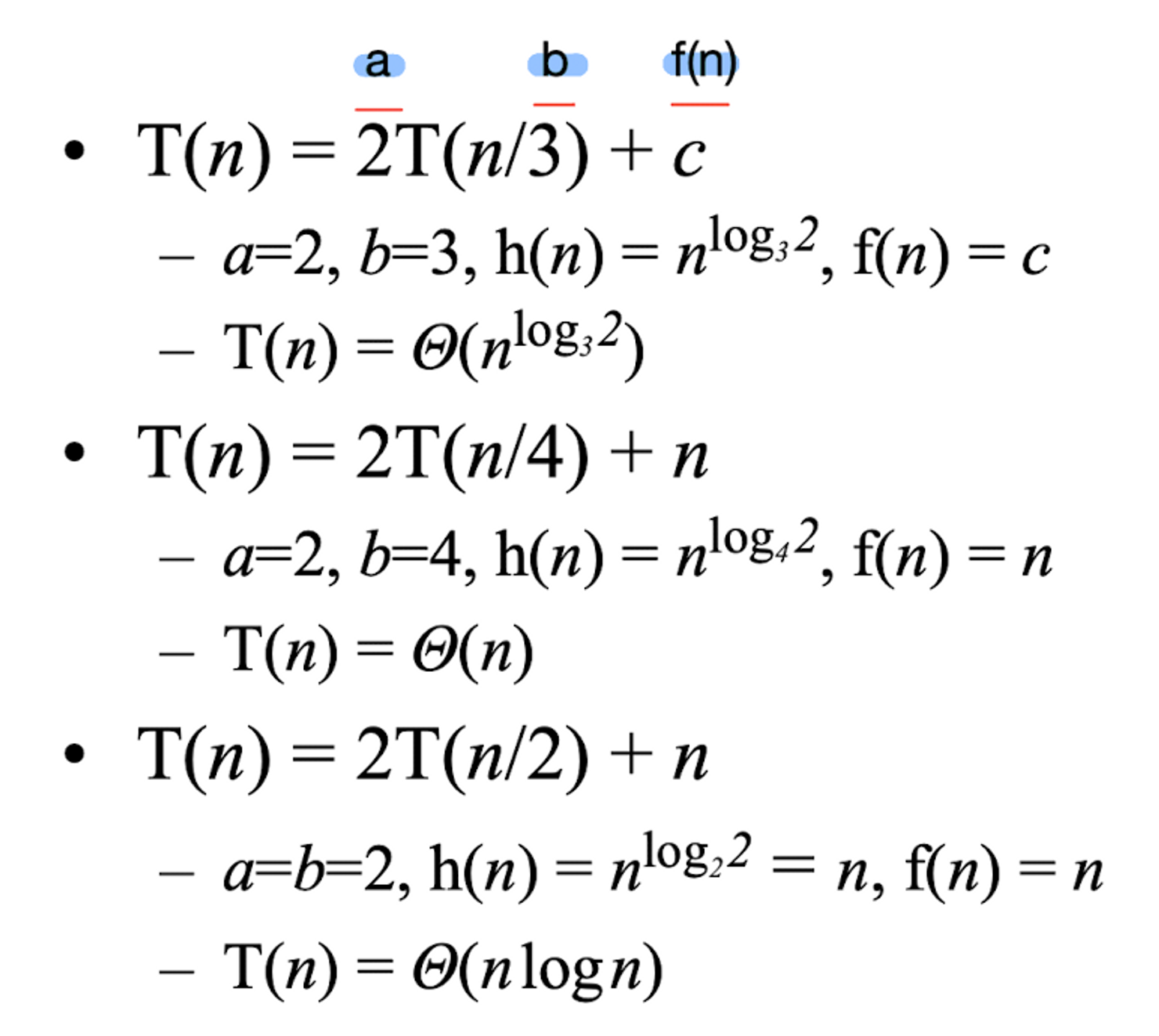
'개발 공부 > 알고리즘' 카테고리의 다른 글
| 알고리즘 | 백트래킹 | Java 백준[Silver II] 꽃길 - 14620 (0) | 2024.09.27 |
|---|---|
| 알고리즘 | 백트래킹 | Java 백준[Silver I] 스타트와 링크 - 14889 (5) | 2024.09.15 |
| 알고리즘 | 조합론 | Java 백준[Silver III] 다음 순열 - 10972 (4) | 2024.09.14 |
| 알고리즘 | 자료 구조 | Java 백준[Silver II] 키로거 - 5397 (1) | 2024.09.08 |
| 알고리즘 | 기하학 | Java 백준[Silver II] 참외밭 - 2477 (0) | 2024.08.24 |



